潮州市2020--2021学年度第一学期九年级数学

期末统测质量分析

 饶平二中实验学校       许伟玉

潮州市教师发展中心    陈  铿

 

一、整体情况

潮州市2020--2021学年度第一学期九年级数学期末教学质量检查，全市有24713学生参加，检查结果平均得分49.6分，优秀率（96分以上）为5.3%，及格率（72分以上）为27.95 %，高分率（108分以上）为0.5%。低分率（60分以下）为60%。以参与本次考试的全体学生数学成绩为总体，本卷难度是0.41。

 

 

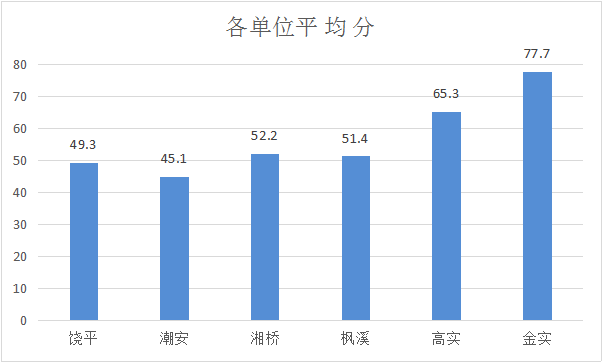
二试卷分析

1.本次试题主要考查以下内容：

	知识内容
	一元二次方程 （28分）	二次函数 （23分）	旋转 （24分）	圆 （32分）	概率初步 （13分）
考查 知识点	一元二次方程的应用；一元二次方程根与系数的关系；解一元二次方程；一元二次方程根的判别式；方程的根	二次函数的性质；二次函数的解析式；函数与不等式；求抛物线的顶点坐标；求二次函数的最大值	中心对称；旋转角；旋转的性质；画旋转后的图形；	圆周角定理；圆锥的侧面积；扇形的面积；计算弧长；垂径定理；切线性质定理；切线判定定理；切线长定理	频率估计概率；概率定义；用列举法求概率；
在本卷 所占比例	23%	19%	20%	27%	11%
能力考查	运算的能力，作图能力，逻辑推理能力。了解学生空间观念、几何直观、数据分析观念和模型思想的培养情况，以及综合应用知识解决问题的能力。

 

2.试卷特点

本试卷以《新课程标准》为依据，结合广东省2020年中考数学试卷的结构形式和进行命题，注重四基考查的同时也充分展示数学的技巧性、灵活性和实用性。从整个试卷来看，考查的知识较全面，类型比较多样灵活，同时紧扣课本、贴近生活。既考查了学生对基础知识把握的程度，又考查了学生的实际应用、计算、思维以及解决问题的能力，不仅顾及了各个层次学生的水平，又有所侧重。这份试题尤其注重对基础知识的检测，以及学生综合运用知识的能力。

3.学生答题情况分析

（1）选择题

选择题（1—10题）部分情况较好，共30分，其中得分率较低的为9、10两小题。第9题涉及“增长率”概念，由于题目表述与平时不同，部分学生无法理解题意导致失分。第10小题考查二次函数的性质与应用，这是函数学习的一个难点，学生失分严重。

（2）填空题

填空题部分，总体完成情况一般，

第11题主要考查解一元二次方程，小部分学生通过约分来求解导致出错，这是对等式基本性质理解不全面的表现。

第12题主要考查了概念的知识，学生完成情况较好。

第13题主要是考查根的判别式，出错的主要原因是没能理解、掌握概念。

第14题考查三角形内心的性质，难度不大，解题的关键是掌握三角形内心是三角形三条角平分线的交点，学生完成得很好。

第15题考查圆锥的计算，根据圆锥展开图扇形的弧长等于圆锥底面的周长列式即可，出错的主要原因是学生没能掌握好计算公式。

第16题考查二次函数的应用，有部分学生得出20或40的错误答案，主要是学生审题不清晰，对“完全停下来，滑行多少米”不理解导致错误。

第17题是对扇形面积公式的考查，由于具有一定阅读量和计算量，学生或是没能正确审题，或是计算出错，因此失分比较严重，只有小部分学生做对。

（3）解答题

第18题考查解一元二次方程，得分率高，只有部分学生在计算结果处理上出错，比如没化为最简二次根式或是忘记变号。

第19题本题考查关于原点中心对称的作图和找图形旋转中心，完成情况较好。第(1)小题是作三角形关于原点的中心对称图形，只有少部分同学没有下结论而失分；第(2)小题是求旋转过程中的旋转中心的坐标，部分学生没能根据旋转的性质找出旋转中心，完成情况一般。

第20题本题考查的是计算简单事件发生概率和用列举法求概率。第(1)小题直接求概率，完成情况好。第(2)小题得分率一般，主要原因是学生审题不清。

第21题主要考查圆的相关知识、等边三角形的判定和性质，以及勾股定理，总体完成情况较好，得分率较高。第（1）小题大多数学生能利用弧等得弦等AB=AC,再由∠ACB=60°得等边三角形，但是有一部分学生证三角形全等，简单问题复杂化。第（2）小题主要是通过作辅助线，利用垂径定理和含有30度角的直角三角形的边角关系，再结合勾股定理求圆的半径，学生主要出现几种错误：①作辅助线描述错误，过点O作OE⊥BC欠垂足；②作垂直后，直接默认点A、O、E在同一直线上；③表达不规范。

第22题本题考查的内容为一元二次方程实际问题的运用，考生的得分率较低，主要失分的原因为：1.审题不清，第（1）小题中“单位价格”误解为“购买总价”；第（2）小题中，大量的学生误认为超过100瓶部分才是新单价；还有部分学生对于“每增加10瓶，单价就降低0.2元”解读不清，没有把x-100再除以10，因此列不出方程。2.答题格式的不规范，没有针对“购买量是否超过100”进行分析，也没有分析根为什么只取200；3.解方程能力偏低，列出正确方程的学生，仅少数能对方程进行化简，并正确解出答案。

第23题本题目主要考查的是旋转的性质，正方形的性质，二次函数的应用及最值。第（1）小题的得分率较高，大部分学生能够通过旋转得到DE=DF，利用SAS证明两个三角形全等。第（2）小题得分率很低，能做出本题的大部分学生是设AE＝x，利用直角三角形面积列出二次函数解析式求最值的方法，但是欠缺考虑，没有证明∠CAF是直角。极少部分同学采用将四边形AEDF的面积转化为△ACD的面积，把△AEF的最大值问题，转化为△DEF的最小值问题，再利用垂线段最短方法求解。更多的错例是将AF当成定长，当AE＝AC时取得最值，造成较多的失分。

第24题为压轴题，是考查圆的知识点，考查的结果不是很理想。第（1）题存在问题主要是错用∠POC=∠POB，PC=PB作为条件证明△POC≌△POB得到90度，说明学生在证全等时依然存在误区；第（2）小题，利用勾股定理或△POD的面积的二种表示方式建立等量关系，从而求出圆的半径。有部分学生利用全等证出两条切线相等，忽视了切线长定理的应用，说明对该知识点掌握不够透彻；第（3）小题做对的同学是非常少的，有个别同学采用做垂直证相似的方法和利用等面积转化获得边长，这个方法非常好。只有极个别同学采用延长两条边相交之后，利用直角三角形斜边上的中线等于斜边的一半进行证明。

第25题为压轴题，主要考查的是二次函数的性质及应用和旋转的知识，难度适中。第（1）小题用待定系数法即可求出二次函数的解析式，得分率最高，第（2）小题通过构建二次函数，利用二次函数的性质求解即可，部分同学因为直线BC的解析式求错，造成后面三角形的底边表达式错误，第二种思路则是多个三角形底和高代入化简后，配方成顶点式错误，从而△BEC的面积最值错误。第（3）小题求点P的坐标。这紧跟了2020年数学中考压轴题的模式，深化了学生对数形结合思想方法即分类讨论的理解和运用，同时又考查了学生的综合分析能力，但由于大部分学生缺乏这种综合分析能力，多数只写出（-1，-2）这一个点。

三、 今后的教学建议：

本次考查的试卷中，全市考生考试的低分率较高，达到60%。说明有一半以上的学生没能很好掌握本次试题考查的相关知识。

另外，本次考试全市考生考试的优秀率（96分以上）和高分率（108分以上）都较低，优秀率5.3%和高分率0.5%。被普遍认为得分率较高的题目，基本都是涉及知识单一，题景传统的题目。被普遍认为得分率较低的题目，基本都是较为综合，表述异于常态，或者是问题关键比较隐秘的题目。说明成绩在及格线（72分）左右的学生对基础知识掌握不扎实，没能实现知识的灵活应用，也反应这部分学生的数学阅读能力、分析问题能力，以及综合应用知识的能力还有待提高。

基于上述情况，在接下来的教学中，我们应该努力做到：

1.      用好三本书，即《数学课程标准》（2011年版）、教材（课本）和教师教学用书，切实领会教材的编写意图，顺应学生的认知规律，选用科学合理的教学方法实施教学，帮助学生真正理解和掌握数学基础知识、基本数学思想，积累基本的数学活动经验。

2.      用实教材（课本）中的每一道例题、练习和习题。通过例题（练习、习题）细致的分析讲解提高学生阅读理解文本、整理分析信息的能力。通过对例题（练习、习题）变式拓展打通知识的关联，帮助学生加深对知识的理解和掌握，提高灵活运用知识解决问题的能力。

3.      作业布置要有针对性，要能针对课堂教学中的难点和重点；作业布置要适量，要让学生有充分的时间去思考；作业布置要分层，尽可能发挥每位学生的潜能；作业反馈要及时，让学生能及时查漏补缺；作业评价尽量个性化，多用激励性评语，激发学生完成作业的动因，保护学生进一步学习的积极性。

4.      要切实做好学困的帮扶和学优生的辅导工作，努力做到“抓两头带中间”。 

对于学困生，要小步子、多台阶，让他们有获得成功的机会，以增强他们学好数学的自信：在设计教学时，在整体的教学目标中，应有一定的阶段性，让学困生能有反馈的机会；在作业及练习布置上，应考虑学困生的基础，加强练习作业的指导。对于学优生，一方面要关注他们合作精神、竞争意识的培养，另一方面要多给他们设置开放性、探究性的问题，让他们在思考、实践、探究中锻炼、提高思维能力和创新能力。